對於區間求和問題，線段樹(segment tree) 可以用來處理區間修改、區間查詢的問題。

像是 731. My Calendar II 這題，每次會標記一個區段，區段內的每個位置最多只能被標記兩次。如果一個區段之內有某個點違反規則，則整個區段的標記會宣告失敗。

這題也可以用前綴和來計算，不過需要不停加總計算，複雜度相對高。

另一個解法就是線段樹了，線段數大致概念是做出一顆二元樹，可以用 ListNode 或者直接開 array 來建造 complete tree（這邊是用 ListNode 來做）。然後在這顆 tree 上紀錄資訊（這個節點底下的範圍、lazy update 的值、目前記錄到的最大 count），並用 lazy update 等技巧稍微優化。

下面努力啃懂後的寫法：

class SegmentTree:
    def __init__(self, u, v):
        self.start = u
        self.end = v
        self.left = None
        self.right = None
        self.max = 0
        self.c = 0

    @property
    def mid(self):
        return (self.start + self.end) // 2

    @property
    def left_tree(self):
        if self.left == None:
            self.left = SegmentTree(self.start, self.mid)
        return self.left
    
    @property
    def right_tree(self):
        if self.right == None:
            self.right = SegmentTree(self.mid+1, self.end)
        return self.right
    
    def lazy_update(self):
        self.left_tree.c += self.c
        self.right_tree.c += self.c
        self.max += self.c
        self.c = 0
    
    def update(self, u, v, x):
        if u <= self.start and v >= self.end:
            self.c += x
            return self.max + self.c
        self.lazy_update()
        if u <= self.mid:
            self.max = max(self.max, self.left_tree.update(u, v, x))
            
        if v > self.mid:
            self.max = max(self.max, self.right_tree.update(u, v, x))
        return self.max
    
    def query(self, u, v):
        if u <= self.start and v >= self.end:
            return self.max + self.c

        self.lazy_update()
        res = 0
        if u <= self.mid:
            res = max(res, self.left_tree.query(u, v))
        if v > self.mid:
            res = max(res, self.right_tree.query(u, v))

        return res

class MyCalendarTwo:
    def __init__(self):
        self.tree = SegmentTree(0, 10**9)
        
    def book(self, start: int, end: int) -> bool:
        if self.tree.query(start, end-1) >= 2:
            return False
        self.tree.update(start, end-1, 1)
        return True

不過如果不是為了學線段樹，其實直接維護兩個 list 的寫法。

class MyCalendarTwo:
    def __init__(self):
        self.once = []
        self.double = []

    def book(self, start: int, end: int) -> bool:
        for s, e in self.double:
            if s < end and start < e:
                return False
        
        for s, e in self.once:
            if s < end and start < e:
                self.double.append([max(s, start), min(e, end)])
        
        self.once.append([start, end])
        return True

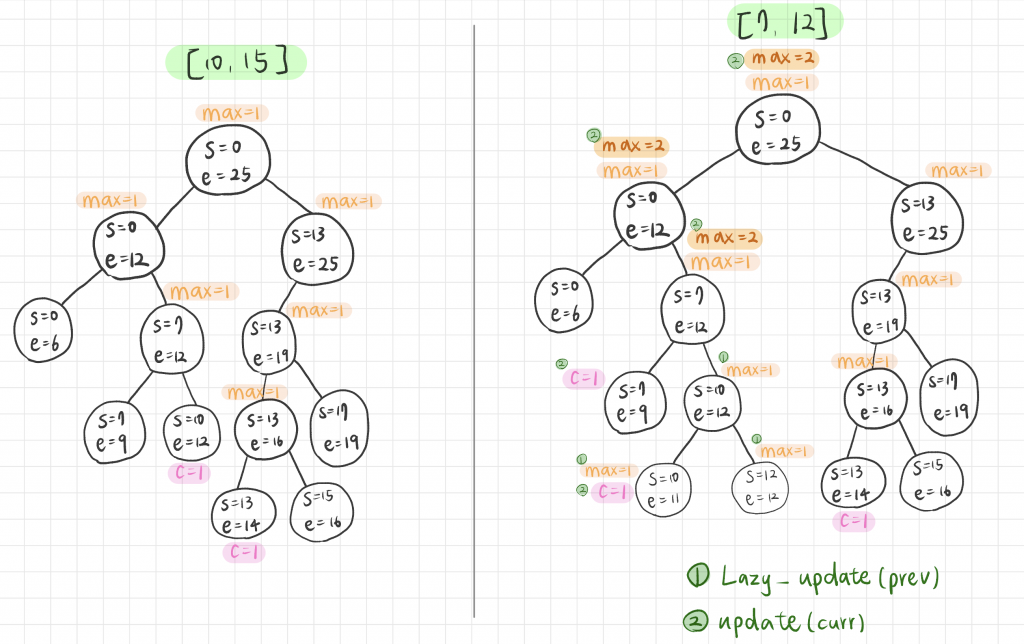
這張圖是我在 trace code 時畫的，假設這顆線段樹的範圍只有 0-25，然後要標記的線段分別是 [10,15] 和 [7,12]（通常都取頭不取尾）。

第一次標記時，query 會把 tree 從原本只有 root 一路切到底，然後 update 會更新最底層 c 和上層 max 的值。

第二次標記時，query 時會進行 lazy_update，把第一次標記的 c 往下層更新。update 則一樣搜尋到最底層，記錄最底層的 c 和上層更新後的 max 值返回。

希望這張圖能稍微有助於理解整個線段樹的運作模式吧。

• 線段樹
  • 731. My Calendar II

• Current count: 5